Le nombre d’or, désigné par Փ (phi), est une star incontestable des mathématiques. Il est encore appelé « section dorée » ou « divine proportion« .

Moins populaire que son pote π auprès du grand publique (faites le test, mais peu de gens peuvent énumérer ses décimales), il n’en reste pas moins plus sexy et plus mystérieux que ce dernier.

Son évocation fait penser aux secrets de la nature, aux arcanes musicales, mais aussi à un savoir-faire architectural ou artistique très secret et confidentiel.

Bref, le nombre d’or sous entend dans l’inconscient collectif, de l’énigmatique et du rêve.

Plutôt pas mal pour un nombre que personne ne retient, hein?

Si vous ne voulez pas vous embêter à retenir un nombre avec l’infini derrière sa virgule (1,618033988749894848204586834…), souvenez-vous que le nombre d’or est défini par sa proportion.

« Le long est au moyen ce que le moyen est au petit. »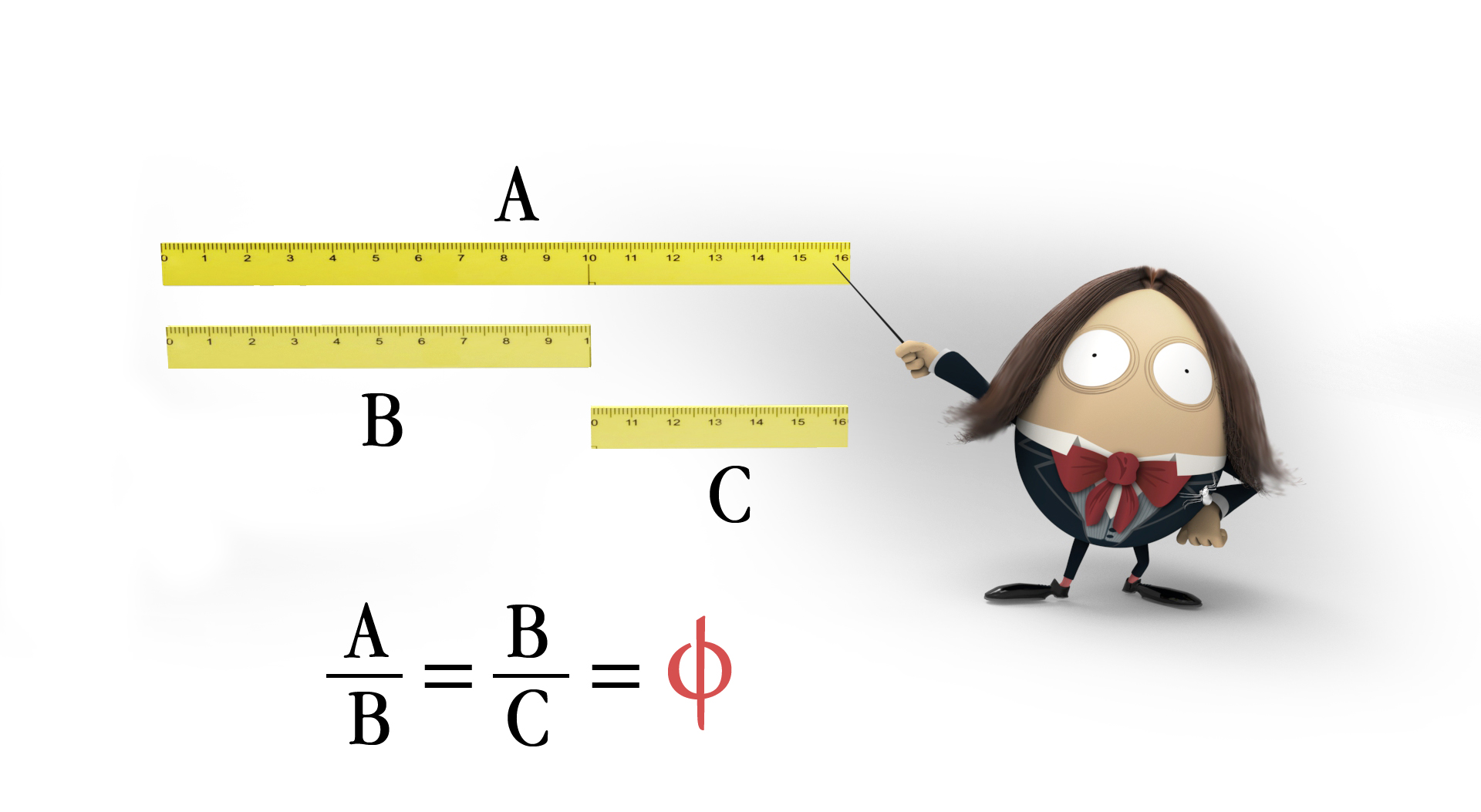

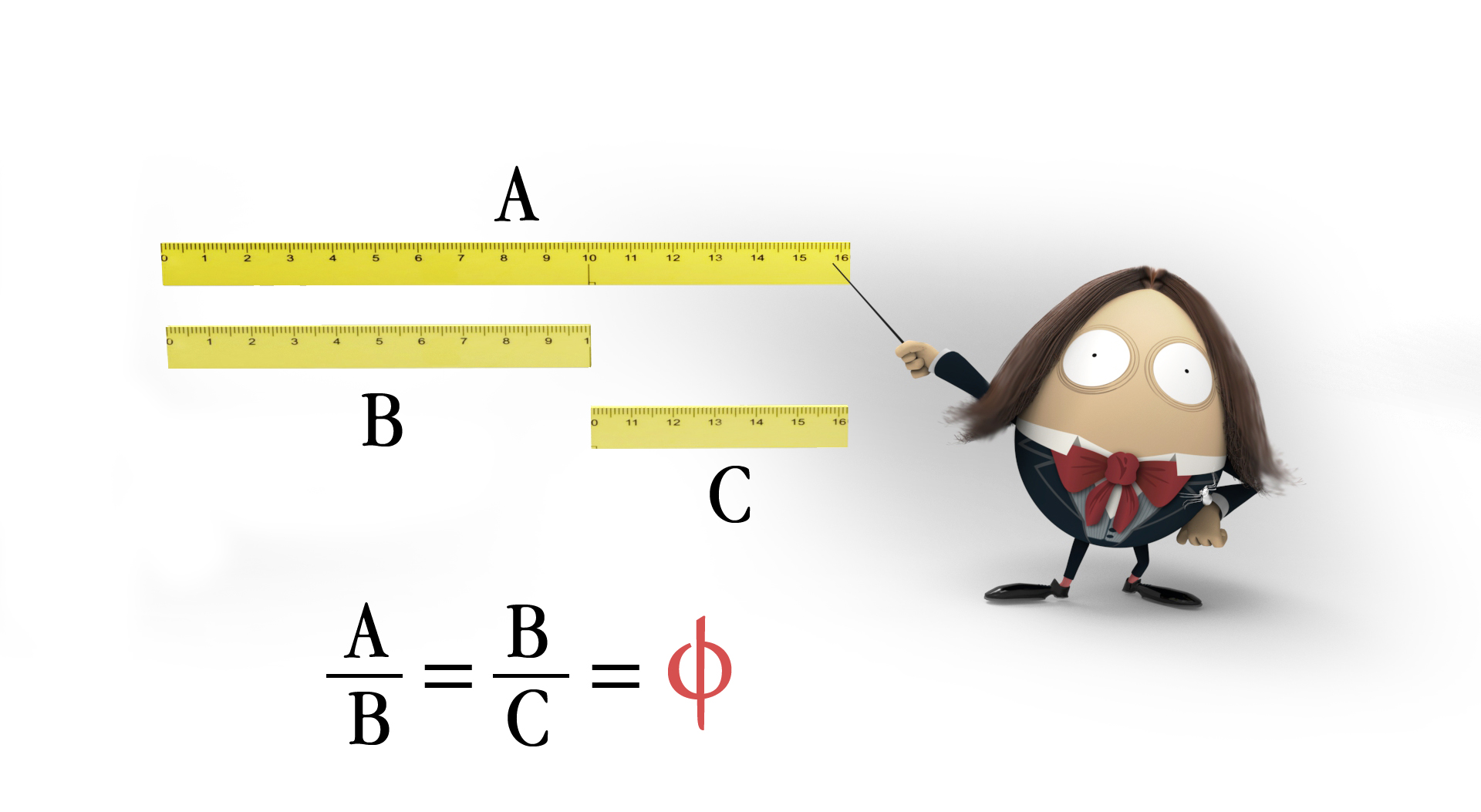
C’est ainsi qu’un segment sera coupé en deux selon la divine proportion.

En gardant cela à l’esprit, vous aurez intégré le concept mathématique du nombre d’or.

De là, va découler la géométrie du nombre d’or avec le rectangle d’or, le pentagone d’or  et la spirale d’or.

 

Rectangle d’or

Si l’on trace un rectangle d’or…

… et que l’on dessine un carré sur l’un de ses grand côté, l’on obtient un rectangle d’or plus grand.

Et l’on peut répéter l’opération indéfiniment…

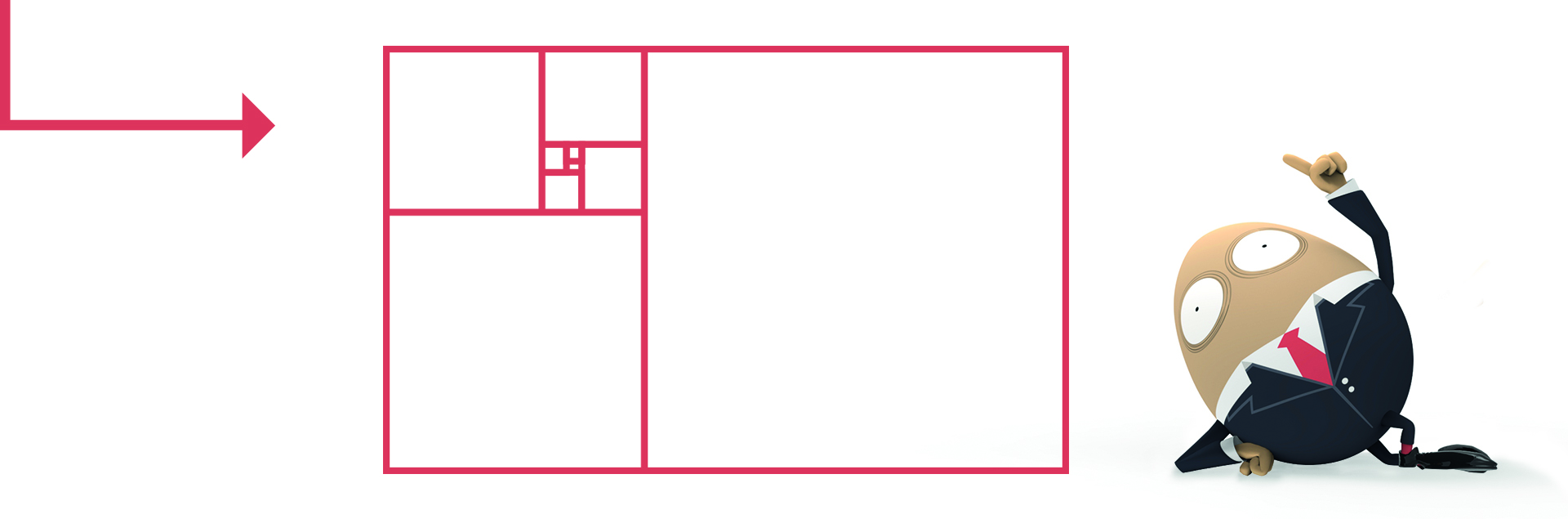
Spirale d’or

Cette suite de rectangle d’or nous permet ensuite de tracer la fameuse spirale d’or. Pour cela, il suffit de la faire circuler, comme ci-dessous, sur les sommets opposés des carrés obtenus précédemment.

Cette spirale Logarithmique se retrouve fréquemment dans la nature. On peut l’identifier chez certains êtres vivants comme les coquillages,  les escargots, les cornes animales et toutes sortes de plantes. Mais aussi dans les phénomènes physiques et naturels, comme la disposition des étoiles dans certaines galaxie, ainsi que les tempêtes, les formations nuageuse ou les cyclones… etc

Le pentagone d’or

Le nombre d’or intervient également dans la géométrie d’une autre figure qui est le pentagone régulier.

Les diagonales de ce pentagone, qui sont au nombre de 5, sont toujours  Փ fois plus grande que ses côtés.

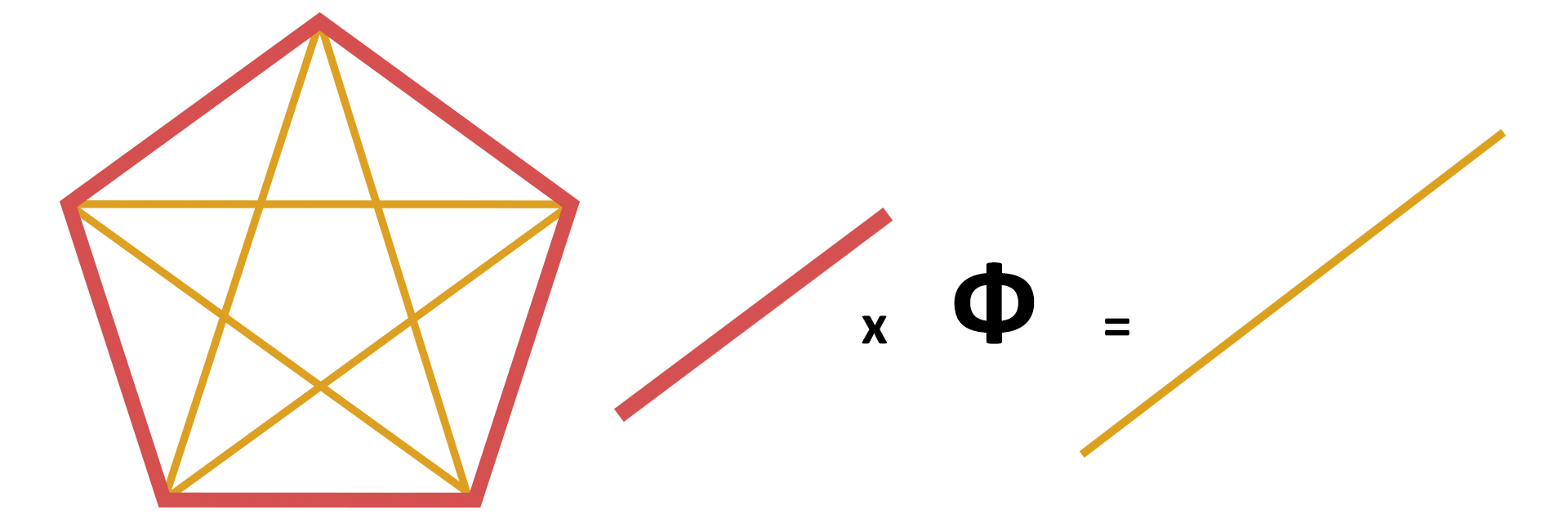
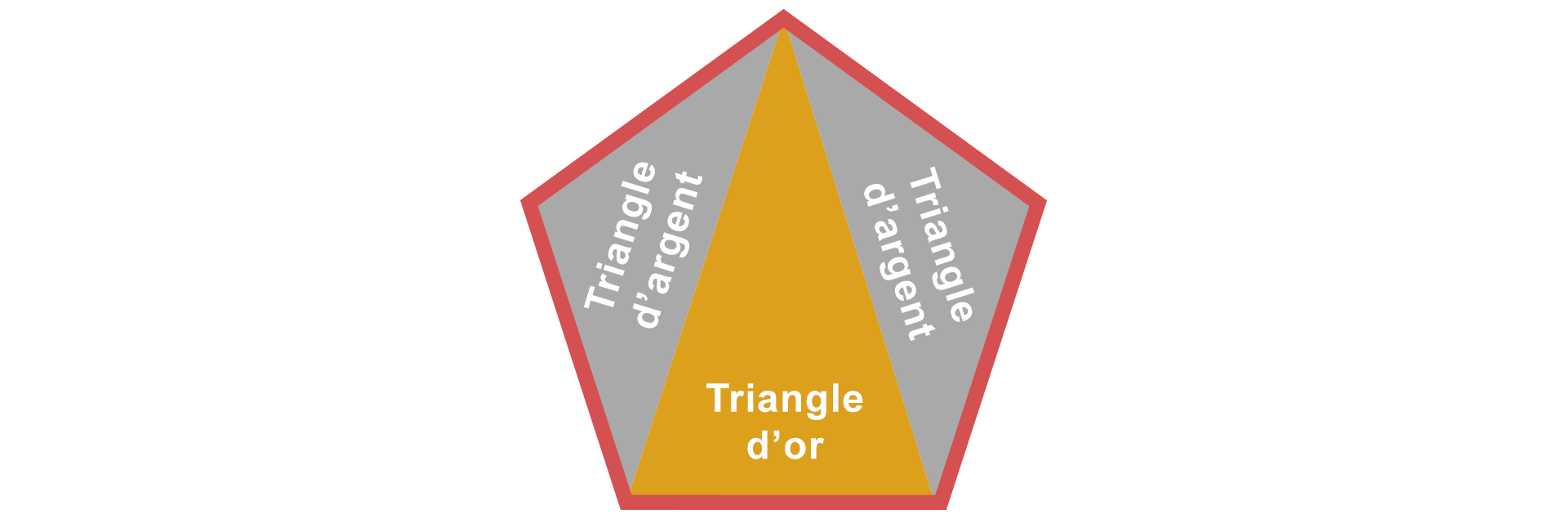
Si l’on trace uniquement 2 diagonales comme ci-dessous, l’on obtient 3 triangles isocèles.

Le triangle au centre est qualifié de triangle d’or. Il est entouré par ce que l’on appelle des triangles d’argent.

Les propriétés de ces triangles leur permettent de remplir un plan de manière apériodique. C’est à dire sans répétition de structure ou organisation particulière.

C’est ce que l’on appelle un pavage de Penrose, du mathématicien du même nom.

Son travail au départ n’était qu’un simple divertissement mathématique pour les fans de Tangram, mais il a finalement été utilisé comme modèle pour étudier la structure de certain cristaux, faisant resurgir une fois de plus le nombre d’or dans les secrets de la nature.

Autres propriétés

En arithmétique, le nombre d’or est le nombre vers lequel converge le rapport entre deux nombres successifs de la suite de Fibonacci.

Cette suite commence ainsi:

1, 1, 2, 3, 5, 8, 13, 21, 34, … pour la faire progresser, il suffit d’additionner les 2 derniers nombres, d’inscrire le résultat et de répéter l’opération.

Si l’on effectue le rapport entre 2 nombres successif comme:

8/5=1,600    13/8 = 1,625     21/13 = 1,615    34/21 = 1,619 …, on s’aperçoit que plus on avance dans la suite de Fibonacci, plus le rapport ces deux nombres converge et se rapproche de la valeur 1,61803…

Ajoutons ceci sur le nombre d’or, il faut savoir que si on le multiplie par lui-même, cela revient à lui ajouter 1.

1,61803… x 1,61803… = 2,61803

Bim! Ca vous la coupe hein???

Pour terminer votre glissade dans notre Tube dédié au nombre d’or, la SlamsOft Corporation vous propose de visionner ce vieux dessin animé de 1959 vachement bien foutu.

La SlamsOft Corporation vous remercie de votre visite et vous souhaite une bonne journée.